이산수학
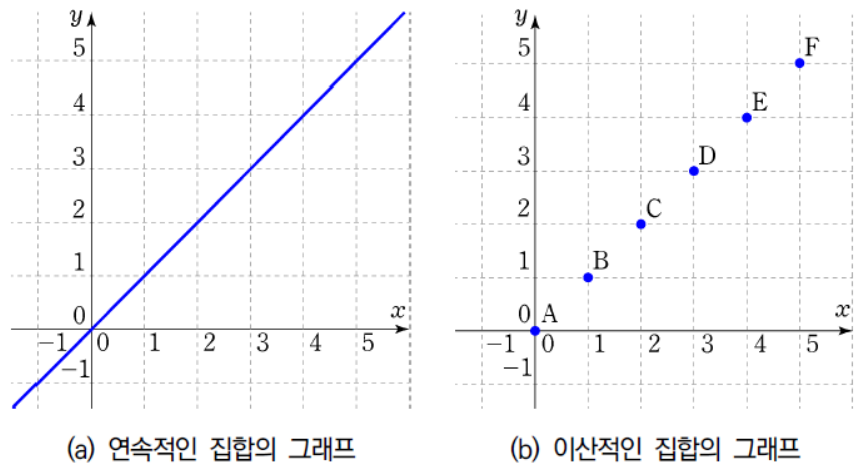
이산적인 수학구조에 대해서 연구하는 학문
이산적 데이터를 처리하기 위해 필요한 수학
연속수학의 반대
모델링과 추상화
도구, 기법, 방법론

방법론: 누가, 언제 어디서, 왜, 어떠한 도구와 기법을 사용해야 하는가에 관한 내용
문제 해결
수학의 도구, 기법, 방법론
- 도구 - 정의, 정리
- 기법 - 가우스 소거법 (일차연립 방정식) - 근의 공식 (2차, 3차 방정식)
- 방법론 - 상황에 따라 가장 효과적이고 효율적인 도구와 기법을 선택하는 것
문제 해결
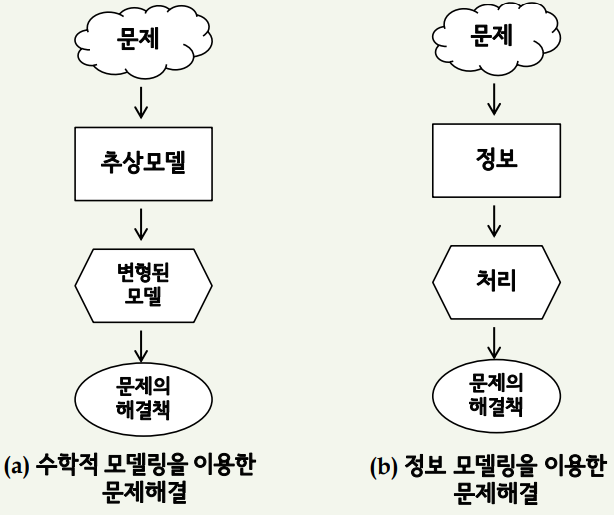
모델링
- 수학적 모델링: 수학적 도구로 실생활의 문제를 해결할 수 있도록 추상화 하는 과정
- 정보 모델링: 실생활의 문제를 컴퓨터에서 해결할 수 있는 형태로 추상화 하는 과정
추상화 abstraction
- 개념을 이미지화 시키는 것
- 핵심만 요약해서 모아놓은 것
- 수학적으로는 문제와 관련된 핵심내용만 남기고 관련 없는 내용을 제거하여 문제를 단순화 시키는 과정


알고리즘 언어
어떠한 문제를 해결하기 위한 여러 동작들의 유한한 모임
알고리즘의 표현 방법
- 컴퓨터 프로그래밍 언어
컴퓨터 작동을 위한 동작을 세밀하게 지시
알고리즘의 핵심요소가 잘 드러나지 않음
중요하지 않은 부차적인 표현에 신경써야 함
통일된 언어가 존재하지 않음 - 순서도

단점: 내용이 복잡하거나 프로그램의 크기가 클 경우에 표현하기 어려움 - 의사코드
모호한 부분은 프로그래밍 언어의 문법을 채용하여 명확하게 기술
구체적으로 표현할 필요가 없는 부분은 자연어를 통해 설명식으로 기술
알고리즘의 작동방식을 설명하는 용도로만 사용
C언어를 기반으로 하는 의사코드 사용

기본 제어구조


이산수학의 응용 분야

자료 출처: 방통대 이산수학 교재
