3. 증명

기본사항

주요 용어

 

정의

공리 (axiom)

어떤 다른 명제들을 증명하기 위해 전제로 사용되는 가장 기본적인 가정으로, 별도의 증명 없이 참으로 이용되는 명제

ex) (1) 두 점이 주어졌을 때, 두 점을 통과하는 직선을 그릴 수 있다. (유클리드 기하학)

(2) 어떤 자연수도, 그 수의 다음 수가 존재한다. (페아노의 공리)

(3) 어떤 것도 포함하지 않는 집합이 존재한다. (공리적 집합론)

 

 

증명 (proof)

특정한 공리들을 가정하고, 그 가정하에 제안된 명제가 참임을 입증하는 작업

 

 

정리 (theorem)

공리로부터 증명된 명제

• 보조정리 (lemma) : 정리를 증명하는 과정 중에 사용되는 증명된 명제
• 따름정리 (corollary) : 정리로부터 쉽게 도출되는 부가적인 명제

 

증명방법

1. 직접 증명법 : 공리와 정의, 그리고 정리를 논리적으로 직접 연결하여 증명한다.
2. 수학적 귀납법 : 자연수 n에 대한 명제의 성질을 증명하는 데 유용한 증명 방법.
   기본단계, 귀납가정, 귀납단계를 이용한다.
3. 간접 증명법 : 증명해야 할 명제를 증명하기 쉬운 형태로 변형하여 증명하는 방법이다.
   대우 증명법, 모순 증명법, 반례 증명법, 존재 증명법 등
4. 그 외 : 전수 증명법, 조합적 증명법, 컴퓨터 이용 증명법

 

직접증명법 (direct proof)

• 다른 말로 연역법(deduction)이라고도 함
  연역법 : 이미 증명된 하나 또는 둘 이상의 명제를 전제로 하여 새로운 명제를 결론으로 이끌어내는 것
• 명제를 변형하지 않고 증명함
• 주로, 공리와 정의, 그리고 이미 증명된 정리를 논리적으로 직접 연결해 증명하는 형식을 따른다.

 

예시

두 홀수의 합은 짝수임을 증명하라.

 

두 유리수의 합이 유리수임을 증명하라.

 

파스칼 삼각형(Pascal’s triangle)

 

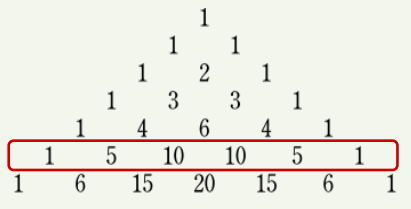
𝒏, 𝒌 는 양의 정수이고, 𝒌 ≤ 𝒏 이라고 가정하면 𝑪 𝒏 + 𝟏, 𝒌 = 𝑪 𝒏, 𝒌 + 𝑪(𝒏, 𝒌 − 𝟏)이다.

 

 

 

수학적 귀납법

모든 자연수 n에 대해 명제를 증명하는 데 유용

 

3단계 과정

• 기본단계 (basis)
  n의 출발점에서 명제가 성립하는가 확인
• 귀납가정 (inductive assumption)
  n = k 일 때 명제가 성립한다고 가정
• 귀납단계 (inductive step)
  n = k+1 일 때도 명제가 성립함을 증명

 

예제

 

 

 

간접증명법 

1. 대우증명법 
2. 모순증명법 
3. 반례증명법
4. 존재증명법

 

대우증명법 (proof by transposition)

𝑷 → 𝑸 ⟺ ~ 𝑸 → ~ 𝑷

 

 

모순증명법 (proof by contradiction)

𝑷 -> 𝑸를 증명할 때 ~ 𝑷를 가정하면 모순이 발생함을 보임

 

 

반례증명법

한정자(quantifer)가 포함된 명제의 증명

 

 

구성적 존재증명법

명제함수 ∃𝒙𝑷(𝒙)를 증명할 때 𝑷(𝒙)를 참으로 만드는 𝒙를 찾거나 찾는 과정을 제시함

 

 

비구성적 존재증명법

명제함수 ∃𝒙𝑷(𝒙)를 증명할 때 𝑷(𝒙)를 참으로 만드는 𝒙 를 찾지 않고 우회적으로 명제가 타당함을 보이는 방법

 

 

다양한 증명방법

전수증명법

명제에서 유도될 수 있는 경우의 수가 적을 때 일일이 모든 경우의 수를 조사하는 방법

 

 

조합적 증명법

두 집합의 원소의 개수가 동일함을 증명할 때 사용됨

• 전단증명
  원소가 n개인 집합 A와 원소가 m개인 집합 B를 찾은 후, 두 집합이 일대일 관계임을 보여 n = m임을 증명함.
• 중복산정
  동일한 집합의 원소를 두 가지 방법으로 센 다음, 그 결과가 각각 n과 m이라면 n = m임을 증명함.

 

컴퓨터를 이용한 증명

증명하기가 복잡한 경우 컴퓨터의 데이터 처리능력을 이용하여 증명함.

 

4색 정리

평면을 유한개의 부분으로 나누어 각 부분에 색을 칠할 때, 서로 맞닿은 부분을 다른 색으로 칠한다면 네 가지 색으로 충분하다.

 

 

 

 

 

 

 

 

자료출처: 방통대 이산수학 강의 자료