2. 논리

명제 Proposition

참과 거짓을 구별할 수 있는 문장이나 수학적 식

 

 

명제의 진리값 (truth value)

• 참 (True), T : 명제가 타당한 경우
• 거짓 (False), F : 명제가 타당하지 않은 경우

 

 

명제의 종류

• 합성명제
• 조건명제, 쌍조건명제
• 항진명제, 모순명제

명제의 진리값 구하기

 

 

---

 

논리 연산

논리 연산자

 

 

합성명제 (compound proposition)

하나 이상의 명제와 논리연산자 그리고 괄호로 이루어진 명제

 

• 논리합 ( disjunction; or, ∨ )
• 논리곱 ( conjunction; and, ∧ )
• 부정 ( negation; ~, ¬ )
• 배타적 논리합 ( exclusive or; xor, ⨁ ): p와 q의 진리값이 t, f로 서로 다를 때
  𝒑⨁𝒒 ≡ (𝒑 ∧∼ 𝒒) ∨ (∼ 𝒑 ∧ 𝒒)    => 동치

배타적 논리합 진리표

 

 

조건명제

조건명제  (conditional proposition, →)

명제 𝒑 와 𝒒 가 있을 때, 명제 𝒑 가 조건의 역할을 수행하고 명제 𝒒 가 결론의 역할을 수행하는 경우

 

𝒑 → 𝒒 ( 𝒑 ⇒ 𝒒)

𝑝는 𝑞의 충분조건

𝑞는 𝑝의 필요조건

조건명제 진리표

 

 

쌍조건명제 (conditional proposition, ↔ )

명제 𝒑 와 𝒒 가 있을 때, 명제 𝒑 와 𝒒 가 조건의 역할과 결론의 역할을 동시에 수행하는 경우

둘 다 T이거나 둘 다 F이면 T
익스클루시브 연산의 not

쌍조건명제 진리표

• 사람이 살아 있다. ↔ 사람이 호흡을 한다.  (T)
• 𝟏 + 𝟐 = 𝟗 ↔ 𝟏 × 𝟐 = 9  (F)

 

 

동치

논리적 동치 (logical equivalence, ≡)

두 명제 𝒑 와 𝒒 가 논리적으로 동등하면 논리적 동치라고 하고, 𝒑 ≡ 𝒒 로 표시한다.

논리적으로 동등하다는 말은 두 명제가 항상 동일한 진리값을 가진다는 의미

𝒑 ↔ 𝒒 ( 𝒑 ⇔ 𝒒, 𝒑 = 𝒒, 𝒑 ≡ 𝒒)

 

 

역, 이, 대우

 

두 논제가 논리적 동치 관계인가?

(1) 𝒑 ∨ (𝒒 ∧ 𝒓)

(2) ( 𝒑 ∨ 𝒒 ) ∧ ( 𝒑 ∨ 𝒓 )

=> O, 분배법칙

 

 

 

or,  ∨ 는 논리합

and, ∧ 는 논리곱

양쪽 화살표는 쌍조건명제

 

 

드 모르간 법칙을 사용해 다음 식의 부정을 나타내시오.

−𝟐 < 𝒙 < 3

 

함축명제 가끔 시험에 출제됨

 

 

항진명제와 모순명제

합성명제를 구성하는 명제의 진리값과 상관없이

(1) 항상 참(T)인 명제를 항진명제라고 한다

(2) 항상 거짓(F)인 명제를 모순명제라고 한다

 

 

---

 

술어논리

술어논리와 명제함수

논리(logic)

• 명제논리 (proposition logic) : 명제
• 술어논리 (predicate logic) : 명제함수

 

명제함수 (propositional function)

변수의 값에 의해 함수의 진리값이 결정되는 문장이나 식

 

 

한정화 (quantification)

전체한정자 (universal quantifier, ∀)

전체한정자는 “모든” 또는 “임의의”를 의미하며, 명제함수 ∀𝒙𝑷(𝒙)와 같이 사용되었을 경우에는 정의역의 모든 [임의의] 𝒙에 대해서 𝑷(𝒙)가 참(T)임을 의미한다.

 

𝑷(𝒙)가 “𝒙는 실수이다”이고 𝒙의 정의역이 양수일 경우 ∀𝒙𝑷(𝒙)는 참

𝑷(𝒙)가 𝒙 𝟐 + 𝒙 − 𝟐 > 𝟎 이고 𝒙의 정의역이 실수일 경우 ∀𝒙𝑷(𝒙)는 거짓

=> 풀이

𝒙^2 + 𝒙 − 𝟐 = 𝒙 − 𝟏 𝒙 + 𝟐 = 𝟎

⇒ −𝟐 ≤ 𝒙 ≤ 𝟏일 때 𝒙^2 + 𝒙 − 𝟐 ≤ 𝟎

∴ ∀𝒙𝑷(𝒙) = F

 

 

존재한정자 (existential quantifier, ∃)

존재한정자는 “존재한다”를 의미하며, 명제함수 ∃𝒙𝑷(𝒙)와 같이 사용되었을 때는 정의역의 어떤 𝒙에 대해서 𝑷(𝒙)가 참(T)임을 의미한다.

 

𝑷(𝒙)가 “𝒙는 무리수이다”이고 𝒙의 정의역이 유리수일 경우 ∃𝒙𝑷(𝒙)는 거짓이다.

 

 

타당성 검사

명제함수의 타당성

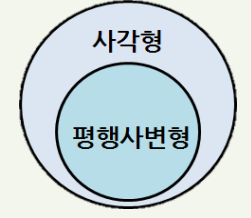
• 벤 다이어그램 (Venn diagram) - 한정자가 사용된 명제함수의 타당성을 직관적으로 검사
  ex) “모든 평행사변형은 사각형이다”

ex) 삼단논법
“영희는 서울에 있다”
“서울은 한국에 있다”
∴ “영희는 한국에 있다”

 

 

---

 

추론

추론 (inference)

참으로 알려진 명제를 기초로 하여 다른 명제를 유도해 내는 과정을 추론이라고 한다.

• 전제: 결론의 근거를 제공하는 알려진 명제
• 결론(conclusion): 새로 유도된 명제

 

유효추론

전제를 참(T)이라고 가정하였을 때 결론이 항상 참(T)이 되는 추론

ex) (( 𝒑 → 𝒒 ) ∧ (𝒒 → 𝒓 )) → ( 𝒑 → 𝒓 )  => 삼단논법

 

 

추론규칙

기본적인 추론규칙은 논리적 동치(항진명제)를 이용함

 

 

예제